RESISTENCIA ELÉCTRICA
Cálculo de la resistencia de un conductor
Sabido que la resistencia eléctrica es la dificultad que ofrece un conductor al paso de la corriente.
Resulta que esta dificultad va aumentando con el camino que tiene que recorrer; es decir, a mayor longitud, mayor resistencia.
Si, por el contrario, se aumenta la sección del conductor, éste ofrecerá menor dificultad al paso de dicha corriente: a mayor sección, menor resistencia.
Se ha comprobado que dos conductores de la misma longitud y de la misma sección, pero distinto material, no ofrecen la misma resistencia eléctrica. Por ello, se llega a la conclusión de que el material del conductor influye en su resistencia.
Para aplicar esta influencia del material en la resistencia, se debe considerar una nueva magnitud que se llama resistividad.
Por tanto, la resistencia eléctrica de un conductor depende de su longitud, de su sección y de su resistividad, y toma como expresión matemática:
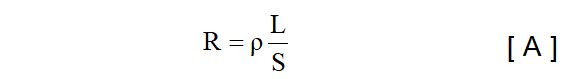
donde:
R = la resistencia (ohmios),
L = longitud (metros),
ρ = factor de resistividad,
S = sección.
RESISTIVIDAD
Resistividad de un material es la resistencia que ofrece un hilo de dicho material de un metro de longitud y un milímetro cuadrado de sección. Se representa por la letra griega ρ (rho).
En la tabla, se pueden ver los valores de resistividad de algunos materiales usados frecuentemente.
CONDUCTÍVIDAD
Es la propiedad contraria a la resistividad, o sea, la facilidad con que los conductores dejan pasar la corriente eléctrica. Se representa por la letra griega σ (sigma), y la relación matemática entre ésta y la resistividad es:
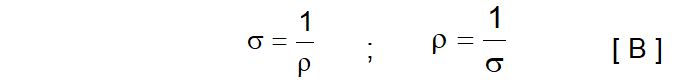
En consecuencia, si se despeja ρ de la expresión [ B ] y se sustituye en la fórmula [ A ], se tendrá:
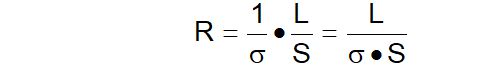
Un material con una resistividad eléctrica alta (conductividad eléctrica baja), es un aislante eléctrico y un material con una resistividad baja (conductividad alta) es un buen conductor eléctrico.
CONDUCTANCIA
El concepto inverso de resistencia se denomina conductancia; indica la mayor o menor facilidad con que la corriente eléctrica atraviesa un conductor. Se representa con la letra G, se mide en siemens y su expresión matemática es:

Ejercicios de aplicación
1º. Se tiene un conductor de cobre de 10 m de longitud y 1 mm2 de sección. Se desea saber su resistencia.
Solución:
Para calcular la resistencia se aplica la fórmula [ A ]:
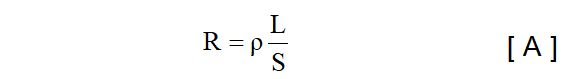
Los valores de la longitud y de la sección vienen dados en el enunciado.
El valor de la resistividad se tiene en la tabla.
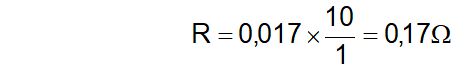
2º. Si se tiene un conductor del mismo material, de igual sección pero de 100 m de longitud, calcular su resistencia.
Solución:
En donde se ve que, siendo del mismo material y sin variar la sección del conductor, la resistencia varia proporcionalmente a la longitud.
3º. Calcular la resistencia de un conductor del mismo material y de una longitud de 10 m, como en el ejemplo 1º, pero con una sección de 2 mm2.
Solución:
En donde se ve que, comparando con el ejemplo 1º, la resistencia es inversamente proporcional a la sección.
4º Si se cambia el material del conductor del ejemplo 1º por aluminio, y se dejan la misma longitud y sección (10 metros y 1 mm2 respectivamente), calcular su resistencia.
Solución:
Se observa, por consiguiente, que manteniendo invariables las dimensiones de un conductor, la resistencia depende del material.
5º ¿Cuál será la conductividad de un conductor si su resistividad es de 0,0172 Ω mm2/m?
Solución:
6º ¿Qué resistencia tendrá un conductor de cobre de 100 m de longitud y 2 mm2 de sección?
Solución:
que es igual que:
Efecto Joule
En la lección anterior, al hablar de resistencia eléctrica, se dijo que ésta dependía de las atracciones de los núcleos sobre los electrones de la corriente, y vimos este fenómeno mediante el roce de los electrones con los átomos. Pues bien, el roce de la corriente eléctrica con los átomos produce, además, un calentamiento del material; por ello, todos los materiales conductores recorridos por una corriente eléctrica se calientan y aumentan su temperatura.
Es evidente que cuanto mayor sea la corriente tanto mayor serán los roces y, por tanto, mayor será el calor producido. Si además el material es muy resistivo (hay una gran concentración de núcleos), habrá más roces y, en consecuencia, aumentará el calor desprendido.
Las unidades caloríficas usadas son: la caloria (cal) y la kilocaloría (kcal)
Caloria: Es la cantidad de calor necesaria para elevar la temperatura de un gramo de agua un grado centigrado.
En el siglo pasado, James P. Joule, físico inglés, estudió la relación existente entre la corriente eléctrica y el calor producido por ésta, y enunció la siguiente ley:
La cantidad de calor producida por una resistencia es igual al producto de la d. d. p. que soporta entre sus extremos por la corriente que la atraviesa y por el tiempo en segundos que circula la corriente, todo ello afectado de un coeficiente de proporcionalidad, de valor 0,24.
La expresión matemática de esta ley es:
Q = (UA – UB) · I · t · 0,24
donde:
Q = cantidad de calor (en calorías),
UA ‑ UB = la tensión en bornes de la resistencia o conductor (expresada en voltios),
I = la corriente eléctrica (en amperios),
t = el tiempo (en segundos).
Esta expresión se puede transformar en otras dos, de uso cotidiano, aplicando la ley de Ohm.
Q = 0,24 · (UA ‑ UB) · I · t
Ya que:
UA ‑ UB = I · R;
y por tanto:
Q = 0,24 · I · R · I · t = 0,24 · I2 · R · t
o también:
Ejercicios de aplicación
1º. Calcular el calor desprendido por una resistencia conectada a 220 V recorrida por una corriente de 2 A, durante dos horas.
Solución:
Se aplica la fórmula:
Q = 0,24 · (UA ‑ UB) · I · t
(Para simplificar, en adelante UA ‑ UB se designará por UAB.)
o sea:
Q = 0,24 · UAB · I · t = 0,24 x 220 x 2 x 7200
ya que 1 hora = 60 x 60 = 3 600 s; y, en consecuencia, 2 horas = 7200s:
Q = 760 320 cal = 760,32 kcal
2º. Qué calor producirá la resistencia de un calentador eléctrico, si su valor es de 40 Ω y está conectado a una tensión de 120 V, durante medio minuto.
Solución:
Se aplica la fórmula:
o sea,
Q = 2,592 kcal
3º Calcular el calor producido por una estufa de 1.000 W, conectada durante 1 minuto.
Solución:
Se aplica la fórmula:
Q = 0,24 · UAB · I · t
pero si se considera que:
UAB · I = WAB
resulta:
Q = 0,24 · WÁB · t y WÁB = 1000 W
luego:
Q = 0,24 x 1.000 x 60 = 14,4 x 103 Cal
Q = 14,4 kcal
Aplicaciones
En todas las aplicaciones eléctricas aparece este efecto calorífico, perjudicial en algunas ocasiones;
Piénsese, en efecto, en los motores, transformadores y máquinas eléctricas, en general; el calor desprendido por efecto Joule es muy peligroso, pues aumenta el riesgo de fallo, por fusión de los aislantes utilizados.
Por el contrario, hay aplicaciones importantes donde se aprovecha ese calor desprendido. Algunas de las más importantes son:
Alumbrado. Soldadura eléctrica y por puntos. Soldaduras blandas, con soldadores eléctricos. Hornos. Estufas y calentadores. Fusibles.
Variación de la resistencia en función de la temperatura
Es importante tener presente que la resistencia no mantiene su valor si se varía la temperatura ambiente o su propia temperatura. Recuérdese que, en la tabla, se daban los valores de la resistividad de varios materiales a 20º C. Esta limitación puede hacer pensar que, a temperatura diferente, serán otros los valores de la resistividad.
Si bien la resistividad varía con la temperatura, lo que interesa destacar es la variación de la resistencia; la expresión o ecuación que determina la resistencia a cualquier temperatura es:
Rt = Ro · (1 + α· Δt)
donde:
Rt = la resistencia a la temperatura t,
RO = la resistencia a 20º C de temperatura,
α = un coeficiente de temperatura,
Δt = Incremento de la temperatura.
En la tabla se pueden observar los valores de la temperatura para las diferentes sustancias.
El aumento de la resistencia con la temperatura se explica por los roces de los electrones con los átomos; si aumenta la temperatura en una resistencia o en un conductor, los electrones se moverán caóticamente y, en consecuencia se producirán más roces con los átomos cercanos, con lo que aumentará la resistencia.
Ejercicio de aplicación
¿Qué resistencia tendrá la bobina de un motor que se ha calentado hasta 70º C, si a 20º C valía 2,5 Ω? La bobina es de cobre.
Solución:
Se aplica la fórmula:
Rt = Ro · (1 + α· Δt)
siendo los datos:
Δt = 70 ‑ 20 = 50 ºC; α = 0,0039; RO = 2,5 Ω
Rt = 2,5 x (1 + 0,0039 x 50) = 2,98 Ω►
Acoplamiento de resistencias en serie
Se dice que un conjunto de resistencias está en serie cuando la salida de una resistencia está conectada con la entrada de la siguiente, y así sucesivamente hasta tener dos únicos bornes que se conectan a la tensión de alimentación.
En un circuito con montaje en serie se cumplen los siguientes principios:
Todos los elementos estan recorridos por la misma intensidad.
La resistencia total es la suma de las resistencias parciales
Rt = R1 + R2 + R3 + ··· Rn
La tensión total es la suma de las tensiónes parciales
Ut = U1 + U2 + U3 + ··· Un
La potencia total es la suma de las potencias parciales
Pt = P1 + P2 + P3 + ··· Pn
Ejercicio de aplicación
A una pila de linterna de 4,5 V se le conectan tres lamparitas en serie de 5, 10 y 15 Ω respectivamente: 1º, hacer el esquema de la conexión; 2º, calcular la resistencia total; 3º, calcular la intensidad de corriente; 4º, calcular la tensión en bornes de cada lamparita; 5º, calcular las potencias parciales en mW y la total del circuito.
Solución:
1. º Se buscan los símbolos de cada elemento en la lista de símbolos, ►
y se prepara el esquema.
2. º La resistencia total será la suma de todas las resistencias:
Rt = R1 + R2 + R3, = 5 + 10 + 15 = 30 Ω
3. º Para hallar la intensidad, se aplica la ley de Ohm al circuito:
4. º Aplicando la ley de Ohm, se obtienen las tensiones de cada lamparita:
U1 = I R1 = 0,15 x 5 = 0,75 V
U2 = I R2 = 0,15 x 10 = 1,5 V
U3 = I R3 = 0,15 X 15 = 2,25 V
Sumando las tensiones de cada lámpara, se obtiene la tensión total aplicada:
Ut = U1 + U2 + U3 = 0,75 + 1,5 + 2,25 = 4,5 V
5. º La potencia parcial en cada lamparita se obtendrá al aplicar la fórmula:
Pp = I · Up.
P1 = 0,15 x 0,75 = 0,1125 W = 112,5 mW
P2 = 0,15 x 1,5 = 0,225 W = 225 mW
P3 = 0,15 x 2,25 = 0,3375 W = 337,5 mW
La potencia total será:
Pt = P1 + P2 + P3= 112,5 + 225 + 337,5 = 675 mW
Y se puede comprobar fácilmente:
Pt = I · Ut = 0,15 x 4,5 = 0,675 = 675 Mw
Acoplamiento de resistencias en paralelo
Se dice que un conjunto de resistencias están acopladas en paralelo o derivación, cuando todas las salidas están conectadas a un punto común, y todas las entradas a otro. A estos puntos se les aplica la tensión de alimentación; por tanto, en un circuito en paralelo todas las resistencias reciben la tensión total y funcionan a la misma tensión.
A diferencia del circuito serie, en el circuito paralelo, como se muestra en el esquema de la figura anterior, la corriente puede circular por varios caminos. En un circuito en paralelo la intensidad total es igual a la suma de las intensidades que pasan por cada resistencia.
It = I1 +I2 + I3
Si se aplica la ley de Ohm al circuito de la figura, se tendrá:
[c]
y corno la corriente que recorre la pila es:
lt = I1 + I2 + I3
se pueden sustituir los valores calculados en [c] obteniéndose:
Al igual que se decía en el apartado anterior, la resistencia equivalente del circuito (Rt) será aquélla que, al colocarla en sustitución de R1, R2 y R3 nos produzca sobre la pila una corriente igual a la It y, por tanto, aplicando la ley de Ohm,
Igualando las dos últimas ecuaciones se obtiene:
Y, simplificando:
Se obtendrá, corno se buscaba, el valor de la resistencia total de un circuito en paralelo:
y generalizando:
El valor de la resistencia total es menor que la resistencia mas pequeña de todas ellas.La formula para el calculo es la siguiente:
Características eléctricas del circuito
Cálculo de las corrientes
Aplicando la ley de Ohm a cada una de las resistencias que componen el circuito y como la tensión de cada una será la de alimentación se tendrá:
Potencia total y potencias parciales
La potencia total absorbida por un circuito derivación es igual al producto de la d. d. p. producida por la pila, multiplicada por la corriente que la atraviesa.
P = U · It
Al igual que sucedía en la conexión serie, esta potencia se reparte entre las distintas resistencias del circuito; se llama potencia parcial la disipada en cada una de las resistencias, siendo su valor igual al del cálculo anterior:
Pp = Ip2 · Rp = Ip U
donde:
Pp = potencia parcial,
Rp = la resistencia en parcial,
Ip = la corriente que recorre dicha resistencia,
U = la d. d. p. del circuito.
Aplicando el principio de conservación de la energía, se obtiene:
P = P1 + P2 + P3
En estos circuitos, al interrumpirse o fallar una de las ramas, el resto sigue funcionando sin deterioro de los mismos.
Ejercicio de aplicación
A una batería de automóvil de 12 V se conectan tres resistencias en paralelo de 6, 4 y 12 Ω respectivamente. Calcular: 1º, el esquema de conexión; 2º, la resistencia total del circuito; 3º, la intensidad absorbida por cada resistencia; 4º, la intensidad total; 5º, las potencias parciales en mW (potencias de 10), y la total del circuito en (W). ►
Solución:
1º Se realiza el esquema de la figura.
2. º Se calcula la resistencia total, mediante la ecuación:
Rt = 2 Ω
3. º Se aplica la ley de Ohm:
Como se ve, resulta que en un circuito en paralelo las intensidades se reparten de forma inversamente proporcional a las resistencias.
4. º A continuación se calcula la intensidad total como la suma de las intensidades parciales:
lt = I1 + I2 + I3 = 2 + 3 + 1 = 6 A
O bien, se aplica la ley de Ohm al circuito:
5. º La potencia parcial se obtendrá aplicando la fórmula: Pp=Ip·U.
P1 = 2 x 12 = 24 W = 24 x 103 mW
P2 = 3 x 12 = 36 W = 36 x 103 mW
P3 = 1 x 12 = 12 W = 12 X 103 mW
y la potencia total se obtendrá de la suma de las anteriores:
P = P1 + P2 + P3 = 24 + 36 + 12 = 72 W
Resultado que se puede comprobar aplicando la fórmula general de la potencia total:
P = U · It = 12 x 6 = 72 W
Circuitos mixtos (serie‑ paralelo)
En la práctica, los circuitos que se presentan con resistencias no son tan simples como los vistos hasta aquí, ya que en general las resistencias se montan por agrupaciones serie ‑ paralelo, esto es, en serie con un circuito paralelo se encuentran una o varias resistencias.
Estos circuitos se llaman mixtos.
Para resolver estos circuitos, se solucionan independientemente los montajes serie y paralelo que lo compongan, con lo que se llega a obtener un circuito único, bien en serie o en paralelo, que se resolverá por el método correspondiente.
Ejercicios de aplicación
1º Calcular en el circuito de la figura la resistencia total equivalente del circuito; b) la intensidad total; c) la tensión en bornes de cada resistencia; d) la intensidad que circula por cada resistencia.
Solución:
a) Se resuelve el circuito en paralelo inferior.
Por tanto, se tiene ya un circuito en serie formado por la resistencia de 5 Ω y la resistencia equivalente del circuito en paralelo.
Rt = R1 + Rp = 5 + 3 = 8 Ω
b) Se aplica la ley de Ohm y se obtiene:
c) Utilizando de nuevo la ley de Ohm (circuito de la figura):
U1=It · R1 = 3 x 5 = 15 V
y:
Up = 3 x 3 = 9 V
y como:
UP + U1 = U ; 15+9=24
d) Las intensidades parciales serán:
En la resistencia R1, por estar en serie en el circuito, la total del circuito:
I1 = It = 3 A
Para calcular la intensidad en las resistencias en paralelo, se aplica la ley de Ohm a cada una de ellas:
2º Calcular en el circuito de la figura: a) resistencia de cada rama; b) intensidad total; c) intensidad de cada rama; d) tensión en bornes de cada resistencia.
Solución:
a) Se resuelve la rama en serie, cuya resistencia es:
RS = R2 + R3 = 4 + 8 = 12 Ω
Queda así un circuito formado por dos resistencias en paralelo ►
(fig.), cuya resistencia combinada es (fig.) ►:
b) Aplicando la ley de Ohm:
c) La tensión en bornes de cada rama será la misma, puesto que están en paralelo. Por tanto:
La intensidad en las resistencias R2 y R3 será igual a la de la rama, puesto que están en serie.
d) La tensión aplicada a cada rama es la de la batería. Por consiguiente:
US = 24 V
U1 = 24 V
U2 = R2 · I2 = 4 x 2 = 8 V
U3 = R3 · I3 = 8 x 2 = 16 V
Ejercicio resumen
Se dispone de un generador de 24 V, al que se acopla un motor cuya resistencia es de 6,3 Ω mediante una línea de cobre de 50 m de longitud y 1 mm2 de sección. Calcular: 1º, resistencia de la línea; 2º, resistencia total; 3º, intensidad del circuito; 4º, tensión en bornes del motor; 5º, potencia cedida por el generador; 6º, potencia absorbida por el motor; 7 º calor disipado por efecto Joule en la línea, sabiendo que ha estado conectado 6 horas; 8º, energía consumida por el motor durante un mes, si cada día está conectado 6 horas.
Solución:
1. º La resistencia de la línea se calcula teniendo en cuenta que se trata de dos conductores, el de ida y el de retorno; y que, por tanto, la longitud del conductor será el doble que la de la línea.
2 º La resistencia total, como se trata de un circuito en serie, será la suma de la del receptor más la de la línea (Fig.):
Rt = RL + RM = 1,7 + 6,3 = 8 0 Ω
3 º La intensidad del circuito se obtiene con la ley de Ohm:
4. º La tensión en bornes del motor se calcula también con la ley de Ohm:
UM = I · RM = 3 x 6,3 = 18,9 V
5 º Con la expresión de la potencia P = U · I se obtiene la potencia cedida por el generador:
P = 24 x 3 = 72 W
6. º Se aplica la misma fórmula anterior P = U · I al receptor:
P = 18,9 x 3 = 56,7 W
7. º Se aplica la fórmula:
Q = 0,24 · I2 ·RL · t
siendo:
RL = 1,7 Ω, I = 3 A y t 6 x 3 600 s
Q = 0,24 x 32 x 1,7 x 6 x 3 600 = 79 315,2 cal
Q = 79,3152 Kcal.
8. º Para calcular la energía consumida en un mes, se calcula, primero, el tiempo de funcionamiento en horas:
6 horas x 30 = 180 horas
Con la fórmula E = P · t, se calcula la energía al mes:
E = 56,7 x 180 = 10 206 Wh ; 10 206 Wh = 10,206 kWh
