MAGNITUDES ELÉCTRICAS

Resistencia eléctrica
►1
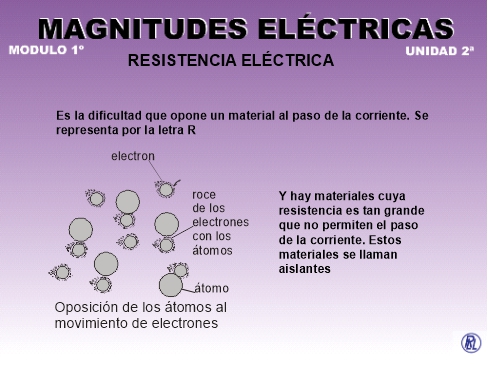
Es la dificultad que opone un material al paso de la corriente. Se representa por la letra R.
►2
Se ha dicho que la corriente eléctrica era una circulación de electrones que se desplazaban a través de los átomos del conductor teniendo que salvar, en su desplazamiento, la acción atractiva de los núcleos de dichos átomos.
A esta dificultad, que dependerá de la constitución atómica del conductor, se le denomina resistencia eléctrica.
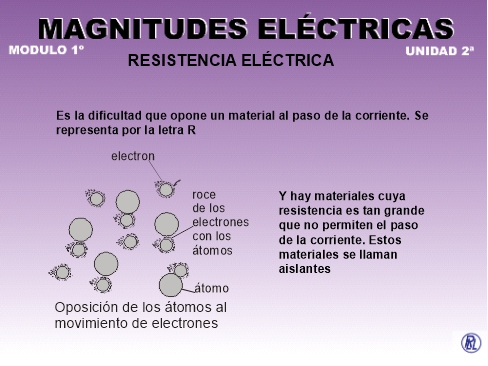
Hay materiales que permiten el paso de la corriente con facilidad y por eso se llaman buenos conductores. Otros ofrecen dificultades y, en consecuencia, se denominan resistivos. Y hay materiales cuya resistencia es tan grande que no permiten el paso de la corriente. Estos materiales se llaman aislantes.
►

Unidad, múltiplos y submúltiplos
►3
La unidad de resistencia es el ohmio y se designa con la letra griega Ω (omega).
►
El ohmio se define como la resistencia que opone al paso de la corriente eléctrica, una columna de mercurio de 106,3 cm. de longitud y 1 mm2 de sección.
►
Para el contraste de resistencias se suele utilizar cajas de resistencias patrones. En muchas aplicaciones, el ohmio no es una unidad adecuada, por ser muy grande en unos casos y muy pequeña en otros; por esta circunstancia, es necesario definir los múltiplos y submúltiplos de ella los cuales se muestran en la tabla con su correspondiente relación
►
Cantidad de electricidad
►4
Es el número total de cargas eléctricas que circulan por un conductor.
Como el electrón, que es la unidad de carga fundamental, es una unidad muy pequeña, ha sido preciso definir otra unidad para los usos prácticos. Esta unidad es el culombio.
El culombio es la cantidad de electricidad que, pasando por una disolución de plata, es capaz de separar 1,118 mg de este metal. Un culombio equivale a la carga de 6,3 x 1018 electrones.
►
La magnitud cantidad de electricidad se representa por la letra Q.
►5
Ejemplo
Calcular la cantidad de electricidad que ha circulado por una disolución de nitrato de plata, si ha depositado en el cátodo (polo negativo) 5,59 gramos de plata pura.
►
Solución:
Se sabe que 5,59 g = 5 590 mg. Si un culombio deposita 1,118 mg, para depositar 5,59 g se necesitarán
►
que equivalen a:
5000 culombios X 6,3 X 1018 = 31,5 X 1021 electrones
►
Intensidad de corriente (medida de la corriente eléctrica)
►6
Es la cantidad de electricidad que recorre un circuito eléctrico en la unidad de tiempo. Se representa por la letra I y se mide con un aparato llamado amperímetro.
►
La unidad de intensidad eléctrica es el amperio, equivalente a un culombio por segundo y que podríamos definir como la cantidad de electricidad que, al atravesar una disolución de nitrato de plata, deposita en el cátodo 1, 118 mg de plata pura en un segundo. Se representa por la letra A
►
►
donde:
Q = la cantidad de electricidad (en culombios).
t = tiempo (en segundos).
I = intensidad de la corriente (en amperios).
Submúltiplos
►7
Al igual que sucedía en el ohmio, el amperio suele ser una unidad o muy grande o muy pequeña, según en las aplicaciones que se usen, utilizaremos los múltiplos o los submúltiplos.
►
EJERCICIOS DE APLICACIÓN
►8
1º Calcular la intensidad de corriente que circula por un circuito si, en 5 horas, 30 minutos y 30 segundos han pasado en total 39.660 culombios.
►
Solución:
Se aplica la formula
►
Q: da su valor el enunciado.
t: se reduce el del anunciado a segundos: t = 5 horas, 30 minutos, 30 segundos
5 horas X 60 = 300 minutos; 300 X 60 = 18.000 segundos
30 minutos X 60 = 1.800 segundos
t = 18.000 + 1.800 + 30 = 19.380
►
►
►9
2º ¿Durante cuanto tiempo ha circulado una corriente habiendo trasportado 2.050 columbios, si la intensidad fue de 2 A?
►
Solución
Se aplica la formula de intensidad, de la que se deduce el valor del tiempo:
►
por tanto
►
►
►10
3º ¿Cuántos miliamperios son 2 A?
Solución
Como 1 mA = 103 A, esto implica que el amperio es mil veces mayor que el miliamperio y, en consecuencia:
1.000mA = 1 A
y, por tanto:
2X 1.000 mA = 2.000 mA
2.000 mA = 2 A
►
►11
4º ¿Cuántos microamperios y miliamperios son 0,0045 A?
Solución
Como:
1 mA = -103 A = 1 A = 103 mA
1 amperio será igual a un millón de microamperios:
1 μA = -106 A = 1 A = 106 μA
por tanto
0,0045 A = 0,0045 X 106 μA = 4.500 μA
0,0045 A = 0,0045 X 103 mA =4,5 mA
►
Fuerza electromotriz. Diferencia de potencial
►12
Siempre que dos cuerpos con distintas cargas están conectados, hay circulación de electrones desde el cuerpo con más carga negativa al de más carga positiva, hasta que se neutralizan eléctricamente.
►
Para cargar un cuerpo, es necesario producir un exceso o defecto de electrones. La energía necesaria para cargar este cuerpo se llama fuerza electromotriz (f. e. m.), con la cual se consigue que el cuerpo adquiera una energía o potencia eléctrica.
►
►13
Si este cuerpo se compara con otro cargado distintamente, se tendrán diferentes energías o potenciales eléctricos; existe entre ambos, por tanto, una diferencia de potencial (d. d. p.).
►
Si se unen, mediante un conductor, estos dos cuerpos, habrá una circulación de electrones desde el de menor al de mayor potencia, tendiendo a igualarse, con lo que cesaría la circulación de corriente. Para mantener la circulación de electrones, hay que mantener la diferencia de potencial mediante un aparato que produzca una f. e. m., al que llamamos generador.
Tanto la fuerza electromotriz E como la diferencia de potencial V se miden en voltios, con un instrumento llamado voltímetro. A la diferencia de potencial se le llama también tensión o voltaje.
►
►14
Símiles hidráulicos
Anteriormente se menciono la igualdad de nombre para corriente eléctrica y corriente de agua; se justifica por la utilización del vocablo corriente. En este apartado se estudiarán las semejanzas entre un símil hidráulico y un circuito eléctrico
Supóngase, primero, que se dispone de los dos depósitos A y B, y de la tubería de unión con su válvula y su turbina. En estas condiciones, al accionar la válvula, se producirá una corriente de agua del depósito A al B, provocando el giro de las paletas de la turbina.
De forma análoga, al accionar el interruptor del circuito, si el punto A está cargado eléctricamente, aparecerá una corriente entre los puntos A y B, transformando su energía en el receptor.
En la comparación de estos dos fenómenos, es fácil identificar la corriente de agua con la de electrones; y el almacenamiento de carga eléctrica en los puntos A y B, con los depósitos. Asimismo, se identifican también la turbina y el receptor, por ser en éstos donde se transforman las energías de las corrientes en otras clases de energías.
Se recordará, como se decía en el apartado anterior, que dos cuerpos cargados con diferentes cantidades de carga se podían comparar entre sí, debido a la relación entre la carga y el potencial eléctrico que poseen.
De esta forma, al observar la figura en el dibujo, se ve que el agua del depósito A está más alta que la del B y, en consecuencia, tiene mayor energía potencial, debido al desnivel entre depósitos.
Por un momento, piénsese en depósitos a la misma altura, sin ningún desnivel entre ellos; si se accionase la válvula, no aparecería ninguna corriente y la turbina no se movería.
Por tanto, se podrá afirmar que la corriente de agua sólo aparecerá cuando los depósitos A y B tengan diferentes energías potenciales.
De forma semejante, se dirá que el punto A del circuito eléctrico tiene mayor potencial que el punto B, siendo ésta la causa de que se establezca la corriente eléctrica.
En un circuito eléctrico se establece la corriente (sentido convencional) desde los puntos de mayor potencial hacía los de menor.
De lo anteriormente expuesto se deduce la analogía entre el desnivel hidráulico y la diferencia de potencial eléctrico.
Por último, al mantener accionada la válvula del circuito hidráulico del depósito A, éste se irá vaciando y, cuando ya no quede agua en él, dejará de existir la corriente de agua. De forma análoga, cuando los dos puntos A y B tengan la misma carga, cesará la corriente.
Por tanto, para mantener el circuito hidráulico en funcionamiento, será necesario que trasvasemos agua desde el depósito B hasta el A nuevamente; esto se consigue con la bomba. En el circuito eléctrico la función similar (creación de cargas) la realiza el generador.
La bomba hidráulica se encarga de que el agua de B adquiera mayor energía potencial, elevándola hasta el depósito A, para lo cual es necesario gastar una energía o realizar un trabajo. El generador eléctrico aumenta también el potencial eléctrico del punto A y, en esta tarea, también se invierte una energía, que es la que se ha llamado fuerza electromotriz (f. e. m.).
Unidad, múltiplos y submúltiplos
La unidad de tensión, voltaje, d.d.p. o f.e.m. es el voltio y se designa por la letra V.
En la práctica, además del voltio, se utilizan dos múltiplos y otros tantos submúltiplos, que son:
►15
Aparatos de medida
►16
Para evaluar las magnitudes eléctricas, se utilizan unos instrumentos que nos indican de forma visible cuáles son las cantidades de electricidad que circulan por un circuito (amperímetro), cuál es el valor de una d. d. p. (voltímetro), o cuánto vale la resistencia que opone un circuito al paso de la corriente eléctrica.
►
Voltímetro
Este aparato, destinado a medir tensiones, está formado por una bobina de hilo muy fino de cobre y gran número de espiras o vueltas; es, por lo tanto, de gran resistencia. Esta bobina es de núcleo hueco y, en su interior, va alojada una pieza de chapa de hierro unida a un eje. Este eje lleva, a su vez, una aguja que se desvía del centro proporcionalmente a la tensión que se aplica a sus bornes, marcando así sobre la escala la d. d. p. existente.
La conexión de estos aparatos se hace en paralelo, ya que tienen que medir
la d. d. p. entre dos puntos de un circuito.
►
Antes de conectar un voltímetro, hay que asegurarse de que la máxima lectura de su escala sea superior a la tensión normal de la red de utilización.
►
►17
Amperímetro
Este aparato, utilizado para la medida de intensidades de corriente, está formado por los mismos elementos del voltímetro, con la diferencia de que su bobina está confeccionada con hilo grueso y con muy pocas espiras. Por tanto, esta bobina es de escasa resistencia
La conexión de este aparato debe hacerse en serie, ya que tiene que medir el paso de la corriente y, por tanto, la desviación de la aguja es proporcional a la intensidad de la corriente.
Este aparato no debe conectarse nunca en paralelo, ya que de hacerlo se provocaría un cortocircuito, en razón de la poca resistencia de su bobina.
►18
Ohmímetro u óhmetro
Este aparato utilizado para la medida de resistencia, está formado por un miliamperímetro con una pila asociada en serie, que es la encargada de proporcionar la corriente que se debe medir
La conexión de este aparato se hace con la resistencia al aire o desconectándola de un punto del circuito sin corriente.
Polímetro ►19
Como su nombre indica, son aparatos para medir diferentes magnitudes con un solo instrumento, pudiendo escoger los diferentes campos y rangos.
Con este instrumento podemos medir tensiones en corriente continua (CC o DC), tensiones en corriente alterna (CA o AC), intensidades en corriente continua (ICC o DCA), intensidades en corriente alterna (CAA o ACA), Resistencias (Ω), en las diferentes escalas.
Para su correcto funcionamiento necesitaremos elegir:
La magnitud a medir
La correcta conexión de las puntas
La escala que más se aproxime (siempre por encima)
Ley de Ohm
►20
Ya se dijo que la diferencia de potencial era la causa de la circulación de los electrones en un circuito. Por consiguiente, a mayor d. d. p., mayor corriente de electrones.
También se vio cómo la resistencia eléctrica es la dificultad que opone un conductor al paso de la corriente eléctrica. Por tanto, si se mantiene constante la causa que hace circular a los electrones, d. d. p., la corriente eléctrica dependerá de la dificultad que oponga el conductor a su paso; esto es, de la resistencia eléctrica.
Experimentalmente, el famoso físico Ohm estableció una ley que lleva su nombre y que dice: En un circuito eléctrico, la intensidad de la corriente que lo recorre es directamente proporcional a la tensión aplicada, e inversamente proporcional a la resistencia que opone el circuito.
►
donde:
U = tensión, I = intensidad, R = resistencia.
►
De esta fórmula, conocidas dos magnitudes del circuito, se puede obtener la tercera.
►
Partiendo de esta ecuación se puede definir el voltio como: la tensión (o diferencia de potencial que es necesario aplicar a un circuito de un ohmío de resistencia para que, por él, circule una intensidad de corriente de un amperio
►
Potencial de referencia (potencial de tierra)
►21
En la mayoría de las aplicaciones prácticas, como punto común para todos los circuitos que componen un aparato, se toma el chasis, que además se conecta a la instalación de puesta a tierra para mayor seguridad contra sobrecargas.
►
Al potencial eléctrico de tierra se le da, por convenio, un valor de cero voltios.
En consecuencia, en un circuito eléctrico, el potencial del punto A tendrá por valor:
UAB = UA-UB = I · R
►
donde:
UA = potencial de A,
UB = potencial de B.
►
y, sustituyendo:
UA – UB = 2 x 6 = 12 V
►
pero el punto B está conectado a tierra y, por tanto, su potencial eléctrico vale 0 V; en consecuencia:
UA ‑ 0 = 12 V = UA = 12 V
Ejercicios de aplicación
►22
1º. Un circuito eléctrico tiene una resistencia de 25 Ω y se le aplica una tensión de 125 V. Calcular la intensidad de la corriente que circula.
►
Solución:
Se aplica la fórmula:
►
►
2º Aplicada al circuito anterior, de 25 Ω de resistencia, una tensión de 250 V, calcular la intensidad de corriente.
►
Solución:
Se aplica la fórmula:
►
de donde se concluye que: A mayor tensión aplicada en un circuito, sin variar la resistencia, mayor intensidad de corriente.
►
►23
3º Aplicada la tensión de 125 V, como en el ejemplo 1º a un circuito de 50 Ω de resistencia, calcular la intensidad de corriente.
►
Solución
De nuevo se aplica la fórmula:
►
de donde se concluye que: En un circuito eléctrico, manteniendo constante la tensión aplicada, la intensidad varía de forma inversamente proporcional a su resistencia.
►
►24
4º ¿Qué tensión será preciso aplicar a un circuito de 6,25 Ω de resistencia para que sea recorrido por una corriente de 20 A?
►
Solución:
Se aplica la fórmula:
U = I · R
U = 20 X 6,25 = 125 V
►25
5º ¿Qué resistencia deberá tener el conjunto de conductor y estufa para que, conectados a una tensión de 220 V. sean recorridos por una corriente de 7 A?
►
Solución:
Se aplica la fórmula:
►
Potencia y energía eléctrica
►26
Fuerza es, en Física, cualquier causa capaz de modificar o producir un movimiento. ►
Ya se ha visto que, para producir el movimiento de electrones, se necesita una fuerza motriz (fuerza electromotriz), que mantenga la d. d. p. la cual, aplicada al circuito, da lugar a la corriente eléctrica.
También la Física define el concepto de trabajo o energía diciendo que: es el producto de la fuerza aplicada sobre un cuerpo por el espacio que le hace recorrer. Sólo habrá trabajo, por tanto, en el caso de que haya movimiento.
►
En electricidad se ha visto que, al aplicar una d. d. p. a un circuito, éste es recorrido por una cantidad de electricidad.
Por consiguiente, se puede decir que en tal caso se desarrolla un trabajo eléctrico E, igual al producto de la d. d. p. aplicada UA ‑ UB multiplicada por la cantidad de electricidad que recorre el circuito Q:
E = Q · (UA – UB)
►27
Si el circuito está interrumpido, no hay posibilidad de movimiento de electrones ni de producción de trabajo eléctrico
►
En un mismo tiempo se pueden desarrollar trabajos distintos. Al trabajo desarrollado, en la unidad de tiempo, se le denomina potencia (P).
►28
Se tendrá más potencia cuando se haya desarrollado un trabajo mayor en el mismo tiempo.
►
Como el trabajo eléctrico lo determina el producto de la fuerza electromotriz por la cantidad de electricidad, la potencia eléctrica P, que es el trabajo eléctrico desarrollado en la unidad de tiempo, será el producto de la fuerza electromotriz, o tensión aplicada, por la cantidad de electricidad que recorre el circuito en la unidad de tiempo:
►
Como a la cantidad de electricidad que recorre un circuito en la unidad de tiempo se le denomina intensidad de corriente, se puede decir que la potencia eléctrica es el producto de la tensión por la intensidad de corriente. Se simboliza con la letra P.
En general:
P = U · I
►29
Diferentes formas de expresar la potencia eléctrica
►30
Por la ley de Ohm se sabe que I = U/R; en consecuencia, sustituyendo en la ecuación anterior se obtiene
o sea:
►31
También de la ley de Ohm se puede obtener otra expresión, ya que sustituyendo U = I · R en la ecuación primera quedará:
P = U · I = I · R · I = I · I · R = I2 · R
►
o sea:
P = I2
· R►
Energía eléctrica
►32
Si a un circuito eléctrico se aplica una potencia durante un tiempo, al cabo del mismo se habrá desarrollado un trabajo o energía eléctrica, igual al producto de la potencia aplicada multiplicada por el tiempo transcurrido:
►
E = P · t
Unidades, múltiplos y submúltiplos
►33
La unidad de la potencia eléctrica es el vatio, que se define corno la potencia eléctrica de un circuito que, al aplicársele una d. d. p. de un voltio, hace circular una intensidad de un amperio; se representa con la letra W.
Vatio = Voltio (V) ·
Amperio (A)
►
En la práctica, cuando las potencias eléctricas son elevadas, se utilizan dos múltiplos del vatio:
►
Otra unidad usada con bastante frecuencia para caracterizar la potencia de los motores eléctricos es el caballo de vapor (CV) o (HP); su relación con el vatio es la misma que en Mecánica:
1 CV = 75 Kg. ‑ cm = 75 x 9,81 W = 736 W
►
La unidad de energía eléctrica es el julio; ahora bien en las aplicaciones prácticas esta unidad es muy pequeña, y se usa como unidad básica el vatio-hora (Wh), que se podría definir como la energía consumida por un receptor durante una hora, sí su potencia es un vatio.
En la mayoría de las aplicaciones eléctricas, la potencia viene expresada en kW y, en consecuencia, la unidad más usada para medir energía es el kWh, que es mil veces mayor que el Wh.
►
Aparatos de medida
►34
La potencia eléctrica se mide con un aparato denominado vatímetro.
Este aparato consta de dos bobinas, una amperirnétrica y otra voltimétrica, que tienen características similares a las del amperímetro y voltímetro.
Debido a las características de las bobinas del vatímetro, se debe poner’ el mayor cuidado en su conexión, pues si no, se corre el grave riesgo de deteriorar el aparato.
►
La energía eléctrica se mide con un aparato llamado contador
►35 ►36
Ejercicios de aplicación
►37
1 º ¿Qué potencia consume un hornillo eléctrico trabajando a 125 V, por el que circulan 2 A?
►
Solución:
Se aplica la fórmula:
P = U · I
P = 125 x 2 = 250 W
►
►38
2 º Una lámpara consume 600 W trabajando a 120 V. Se desea saber la corriente que circula y su resistencia.
►
Solución:
Se utiliza la fórmula P = U · I de la que se despeja el valor de I:
►
Para calcular la resistencia se aplica la ley de Ohm:
►
►39
3 º Si una estufa consume 2 kW y tiene una resistencia de 25 Ω, calcular la tensión de trabajo e intensidad de consumo.
►
Solución:
Se toma la expresión de la potencia según la ecuación de la que se despeja el valor de U.
►
El valor de la intensidad se calcula por la ley de Ohm:
►
►40
4 º Calcular la potencia de un hornillo de 20 Ω de resistencia, cuya tensión de funcionamiento es 100 V.
►
Solución:
Este problema se puede resolver de dos maneras:
1 ª Aplicando directamente la ecuación:
►
2 º Aplicando la ley de Ohm:
►
luego la potencia consumida será:
P = U · I = 100 x 5 = 500 W
►
►41
5º. Un calentador eléctrico de 120 V de tensión nominal, consume 2 A. Si está conectado durante 3 horas, calcular la energía consumida en Wh y en kWh.
►
Solución:
Se calcula primero la potencia del aparato:
P = U · I = 120 x 2 = 240 W
►
Sabido el tiempo que está trabajando, se calcula la energía:
E = P · t = 240 x 3 = 720 Wh = 0,72 kWh
►
►42
6º. ¿Qué tiempo tarda una lámpara de 50 W en producir 3,5 kWh?
►
Solución:
Primero se pasa el valor de la energía a Wh:
3,5 kWh = 3 500 Wh
►
Como se sabe que E = P · t, se despeja el valor del tiempo:
►
►43
Ejercicio resumen
Se tiene una estufa eléctrica que funciona a la tensión de 220 V y cuya resistencia es de 44 Ω. Calcular: 1º, la intensidad de corriente; 2º, la potencia de dicha estufa; 3º, la energía consumida al cabo de un mes, si está enchufada durante 6 horas diarias. El resultado en kWh.
►
Solución:
1º Aplicando la ley de Ohm, se tiene:
►
2º Conociendo la tensión e intensidad de funcionamiento se obtiene el valor de la potencia:
P = U · I = 220 x 5 = 1100 W
►
O también
►
►44
3º Se calcula, primero, el tiempo que esta funcionando durante un mes:
30 días X 6 horas diarias = 180 horas
►
Se calcula, a continuación, la energía: E = P · t, poniendo previamente la potencia en kWh: 1100 W = 1,1 kW.
►
E = P · t = 1,1 X 180 = 198 kWh
►
45►
